音声あるいは一般的な音の基礎知識

音の発生

音が存在するためには、振動するものとそれを伝える媒体が必要です。具体的には 音は通常、媒質としての空気の圧力変化として伝わります。マイクロフォンは音声を電気信号の変化としてとらえます。アナログレコードやカセットテープはこの電気信号をそのまま記録しています。音声は時間と共に変化する信号です。

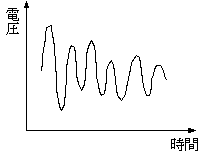
デジタル記録

音の各瞬間の波形の値を数値として記録します(A/D変換)。非常に短い時間間隔Δt で記録していけば、数値から音を再生できます(D/A変換)。数値には16ビットの値 (0〜65535) がよく使われています。

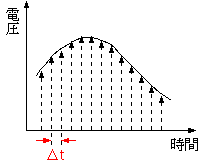
人間の耳で聴きとれる周波数は20Hz〜20kHzと言われています。サンプリング定理(量子化定理)によると、元の波形を正しく再生するには、量子化したい元の波形の周波数の最低2倍のサンプリング周波数が必要となります。このため、デジタル音声では、44.1kHz(CD)と48kHz(DAT)のサンプリング周波数が主に利用されています。

音楽用のCDに必要なデータ量を計算してみましょう。

音楽用CDは、左右2チャンネルで、サンプリング周波数44.1kHz、16ビットで量子化されています。

1秒間の音声データを録音するために必要なデータ量は、
2 x 44.1x103 x 16 = 1411200 (ビット)
となります。
CD1枚には最大74分記録可能です。 CDに記録可能なデータ量はいくらになりますか?

D/Aコンバータ

デジタル信号を、アナログ信号に変換する装置です。たとえば、CDプレーヤーでは、内蔵されているD/Aコンバータで、デジタルデータをアナログに変換しています。 PCでも音声の再生時に、デジタル信号をアナログ信号に変換しています。 D/Aコンバータには、 16bit、20bitなどのマルチビットタイプと、1bitタイプがあります。

A/Dコンバータ

アナログ信号をデジタル信号に変換します。コンピュータはアナログ信号を直接扱うことができないため、デジタル信号に変換する必要があります。 PCでは、音声の録音時に、アナログ信号からデジタル信号に変換しています。 A/Dコンバータには、扱うことができるビット数によって、8bit、16bitといった数が用いられ、数字が大きいほど精度が高くなります。

PCM (Pulse Code Modulation)

アナログの音声データを変換してデジタル化して記録し、再生の際にアナログデータに変換する方式のひとつです。
アナログ量を一定の周期で取り出すことをサンプリングといいます。サンプリングされたデータを量子化し、さらに2進数に変換します。音声の場合は、サンプリング周波数により音の高低が決まり、量子化ビット数により音のダイナミックレンジが決まります。サンプリング周波数が高いほど原音に忠実な再生が可能ですが、データ量は大きくなります。
音楽用CDやCD-ROMなど、さまざまなメディアに利用されています。 CDの場合は 44.1kHzでサンプリングされ、16ビットで量子化されます。 DATの場合は 48kHzでサンプリングされます。 PCMデータを再生する音源をPCM音源と呼び、最近のPCには標準で内蔵されています。

ADPCM (Adaptive Differential Pulse Code Modulation)

アナログの音声データを圧縮してデジタル化します。サンプ ルデータの差分をとって圧縮することにより、PCM に比べてデータ量を減らすことができます。

WAVファイル

WindowsのPCM音声の標準形式ファイルです。

周期を持った波形

音の3要素は、音の高さ (Pitch)、音色 (Tone)、音量 (Volume)です。周期を持った波形は、ある一定周期で同じ形が繰り返されます。 1秒間に何回繰り返すかが周波数 f [Hz] です。周期T [s]はfの逆数です。音の高さは、周波数が高いと高い音、低いと低い音になります。

次は、音色について考えてみましょう。波形の最も基本的なものは正弦波です。

フーリエ級数展開は勉強しましたか。フーリエによれば、基本波に適当な周波数の高調波を選択し、その振幅を調整し加えてやることで、 理論的には全ての波形を作ることができます。どんな周期関数であっても、三角関数の足し算のみで表現できます。

まず、基本になる音の高さ(ピッチ) を決めます。例えば、周波数f=440Hz (ラの音) とします。 この基準になる音を基本波と言います。これに、正弦波を足し合わせていきます。すると、周波数f=440Hzの音の高さで、さまざまな音色を作ることができます。

基本波(基音: Fundamental) に足し合わせる 正弦波のことを、第n調波(倍音: Overtone) と言います。 基本波の周波数をf=440Hzとすると、

基本波 第2調波 第3調波 第4調波 第5調波 ・・・ 第N調波 ・・・
周波数 440Hz 880Hz 1320Hz 1760Hz 2200Hz ・・・ 440 x N Hz ・・・

となります。 それぞれの調波の振幅は基本波の振幅より小さくします。

これは ノコギリ波と呼ばれる波形のスペクトルで、すべての整数調波を含みます (ノコギリ波には、up と down の二種類があります)。

基本波 第2調波 第3調波 第4調波 第5調波 ・・・ 第N調波 ・・・
周波数 440Hz 880Hz 1320Hz 1760Hz 2200Hz ・・・ 440 x N Hz ・・・
大きさ 1 1/2 1/3 1/4 1/5 ・・・ 1/N ・・・

以下に、基本波、第2〜5調波までの関係を示します。このように高調波を足していくとノコギリ波(down)に近付いていきます。

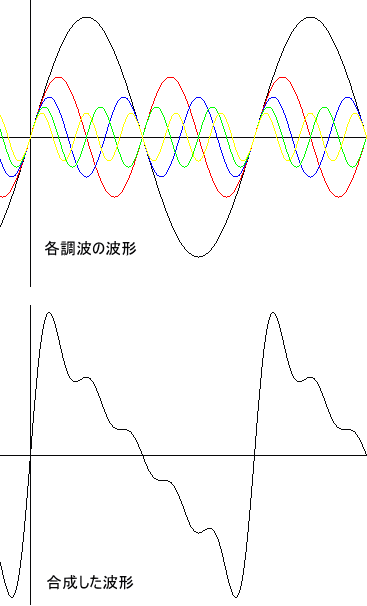
もう一つシンセサイザーの音作りに欠かせない波形として、矩形波があります。 これは、長方形の形をした波形で、 整数調波のうち、 奇数次調波のみを足し合わせていきます。

基本波 第3調波 第5調波 ・・・ 第(2N-1)調波 ・・・
周波数 440Hz 1320Hz 2200Hz ・・・ 440 x (2N-1) Hz ・・・
大きさ 1 1/3 1/5 ・・・ 1/(2N-1) ・・・

しかし、このような加算方式で波形を合成することは現実的ではありません (無限調波まで演算できない)。このため、ほとんどのシンセサイザでは 減算合成方式を使用します。ノコギリ波や、矩形波を生成し、その後、いらない倍音成分をフィルタを通して削り落し、音色を合成します。

参考のために、歪み波の波形アプレットはこちらです。

フィルタ

フィルタは、定められた周波数範囲だけを通過させ、それ以外の周波数を遮断するものです。 フィルタは特性によって次のように大別できます。 これらのフィルタの理想的な振幅特性を示します。ただし、実際のフィルタの特性はこの図のようにきれいにスパッとは切れません。

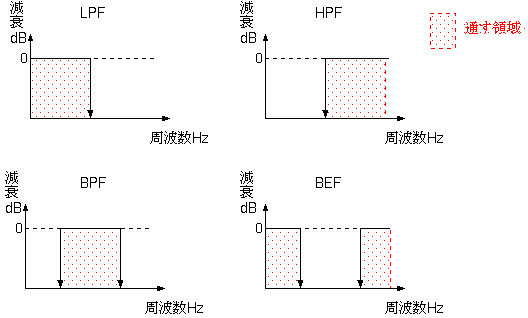
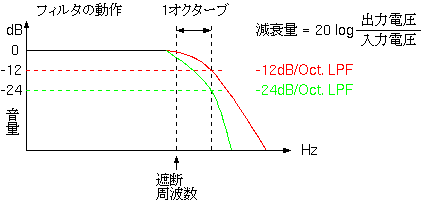
たとえば、同じ遮断周波数の二種類のLPFを示します。一つは、遮断周波数から1オクターブ高い周波数が-12dBに減衰するLPFで、もう一つは、-24dBに減衰するように設計したLPFの例です。

トップページに戻る